Intertia Ball 1F20.10
Mechanics Newton's First Law Inertia of Rest

Concept

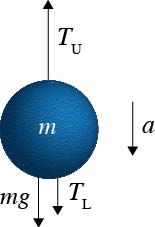
In the free-body diagram, let $T_L =$ lower string tension, $T_U =$ upper string tension. Choosing all forces and the acceleration downwards as positive, Newton’s Law gives:

$$\begin{align*} T_L + mg − T_U &= ma \\ \\ \frac{T_L − T_U}{m} &=a−g \end{align*}$$

We thus have three cases, each distinguished by how the resulting acceleration compares to $g$:

  1. $T_L< T_U$, so $a < g$ and the upper string breaks
  2. $T_L= T_U$, so $a = g$ and the two strings break simultaneously (heretofore unobserved)
  3. $T_L > T_U$, so $a > g$ and the lower string breaks

Note that a quick jerk on a full roll of toilet paper provides a similar result.

Procedure

  1. Place the bar through the bottom loop of the string hanging from the ball.
  2. Hold each end of the bar making sure your hands are not directly below the iron ball.
  3. Poll the class as to which string will break as the result of a very slow pull.
  4. Pull the bar down very slowly.
  5. Notice the upper string breaks and the ball falls.
  6. Replace the broken string with one of the provided extra strings.
  7. Repeat steps 1-2, but this time jerk the bar down quickly.
  8. Notice that the lower string breaks and the ball remains suspended.

Equipment

  1. Suspension Platform
  2. 30 cm Bar
  3. Iron Ball with Hooks
  4. (4) 6 inch End-Loop String