

Concept
Here is a classic textbook application of Newton’s Laws. The analysis of forces and torques on the two masses and pulley gives:
$$\begin{align} m_{2} g − T_2 &= m_2 a \\ T_1 − m_1 g &= m_1 a \\ R(T_2 − T_1 ) &= I\alpha \notag \\ &= I \frac{a}{R} \notag \\ &= \beta m_p R^2 \frac{a}{R} \notag \\ R(T_2 − T_1 ) &= \beta m_p R a \end{align}$$
Solve Equation (1), (2) and (3) to obtain the system’s acceleration:
$$\begin{align} a = \frac{(m_2 - m_1)g}{m_1 + m_2 + \beta m_p} \tag{4} \end{align}$$
Note: Equation (4) is the net force on the system divided by its total mass, where $\beta m_p$ is the effective rotational inertia of the pulley.
For constant acceleration the time to fall a distance h from rest is:
$$\begin{align} t=\sqrt{\frac{2h}{a}}\tag{5} \end{align}$$
In the example where $h =$ 100 cm, $m_1 =$ 500g, $m_2 =$ 550g, $β =$ 1, $m_p =$ 10g,and $g = 980\text{cm/s}^2$, Equation (4) and (5) give $t =$ 2.1 s.
Since $β m_p << m_1 + m_2$, the effect of the pulley may be neglected if desired.
Procedure
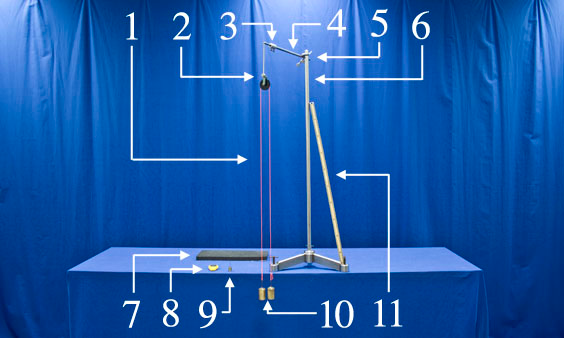
- Verify that the 500g weights are hanging from each end of the string that is suspended from the pulley.
- Ask for a volunteer to act as a timer.
- Hang the 50g weight from the base of one of the 500g weights.
- Use the meter stick to hold the 550g weight 1 meter above the foam platform.
- As you release the weight, the volunteer starts the stopwatch.
- The volunteer stops the stopwatch when the weight touches the foam platform.
- Verify that the measured time (~2 seconds) matches the calculated time (2.1 seconds).
Equipment
- String
- Suspended Pulley (10g disk)
- Straight Rod Clamp
- 1.5ft Rod
- Large Rod Clamp
- Large Stand
- Foam Platform
- 50g weight
- (2) 500g weights
- Meter Stick