


Concept
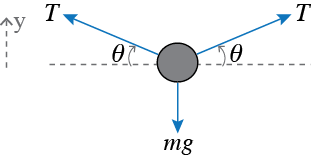
Application of Newton’s Law to the free-body diagram, where $T =$ tension, gives:
1. $\sum F = T sin\theta + T sin\theta − mg = m a_y = 0$
2. $T = \frac{mg}{2 sin\theta}$
Eq. 2 indicates that for $\theta \approx 30°$ as in the photograph, $T \approx mg \approx (11 kg)(9.8\text{m/s}^2 ) \approx 110$ N.
Eq. 2 also shows that as $\theta \rightarrow 0$, i.e., the rope approaches the horizontal, that $T \rightarrow \infty$. Thus, it is impossible for the rope to be horizontal, even if the only weight to be supported is the rope's own weight.
Procedure
- Ask the audience for two strong volunteers.
- Ask them if they think they can apply enough tension to the rope to make the rope horizontal.
- Have each volunteer pull on opposite sides of the rope trying to make the rope as horizontal as possible.
- Estimate the rope’s minimum angle with respect to the horizontal that they are able to make.
- Calculate the maximum tension that the volunteers were able to apply to the rope.
Equipment
- Thick Rope
- Large Water Bottle (11 kg)