Pulling on The Whirligig 1Q40.25
Mechanics Rotational Dynamics Conservation of Angular Momentum

Concept

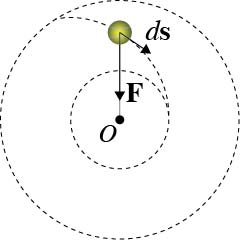
Here’s a simple example of central force motion similar to the Earth’s orbit around the Sun. The characteristic dynamics are such that the rotating whirligig, like the Earth, does not have any torque exerted on it by the centripetal force, and hence angular momentum is conserved

This can be seen in the diagram displayed. As the whirligig is pulled in, the tension in the string supplies a centripetal force $\mathbf{F}$, directed towards point O. Since this force acts along a line extending through the rotation axis about point O, $\mathbf{F}$ cannot exert any torque on the whirligig. Hence, angular momentum is conserved.

In contrast, there is a component of $\mathbf{F}$, parallel to the displacement, $d\mathbf{s}$, such that $\mathbf{F} \cdot d\mathbf{s} > 0$. So, the string tension does work on the whirligig, increasing its kinetic energy. This is clearly manifested in the obvious increase in the whirligig’s linear speed. Because the angular momentum, $m v r = m (\omega r) r = m \omega r^2$ is constant, as the whirligig is pulled in and $r$ decreases, the angular speed ω, like the linear speed, must also increase.

Procedure

  1. Hold the nylon tube with one hand and swing the ball in a circular motion above your head.
  2. Pull down on the ring attached to the opposite end of the string to adjust the ball’s radius of revolution.
  3. Notice that the ball’s instantaneous velocity increases as its radius of revolution decreases.

Equipment

  1. Whirligig