Green's function for the Diffusion equation

We show that the Green's function for the diffusion equation,

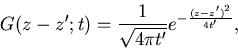$$G(z-z';t)=\frac{1}{\sqrt{4 \pi t'}}e^{-\frac{(z-z')^2}{4t'}},$$ (35)

satisfies the equation and behaves like a delta function at t'=0.

Plugging the Green's function into the canonical diffusion equation, Eq. 16, gives on both sides

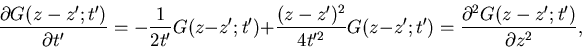$$\frac{\partial G(z-z';t')}{\partial t'}= -\frac{1}{2 t'} G(z-... ...4t'^2} G(z-z';t')= \frac{\partial^2 G(z-z';t')}{\partial z^2},$$ (36)

verifying that it is a solution to the equation.

As $t' \to 0$, for $z \neq z'$, the argument of the exponent goes to $-\infty$, and $G(z-z';t') \to 0$. For z=z', it goes to infinity as $t' \to \infty$. The integral over z' can be found by substituting $q=(z-z')/\sqrt{2t'}$ and gives

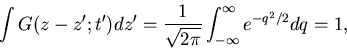$$\int G(z-z';t') dz'= \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} e^{-q^2/2} dq =1,$$ (37)

showing that it is correctly normalized to be the solution for a delta function source or point source at z=z' when $t' \to 0$.